BioMed Foundation

< All Topics

03.06 Summary Chapter

Posted04/01/2025
Updated04/01/2025
ByBMF
Views27

1. Chemical Formulae

a. Molecular Formulae

  • Definition: Represents the actual number of atoms of each element in a molecule.
  • Representation: Uses chemical symbols from the Periodic Table with subscripts indicating the number of atoms.
  • Diatomic Elements: Seven elements exist as diatomic molecules (X₂): Hydrogen (H₂), Nitrogen (N₂), Oxygen (O₂), Fluorine (F₂), Chlorine (Cl₂), Bromine (Br₂), and Iodine (I₂).

b. Empirical Formulae

  • Definition: Simplest whole-number ratio of atoms in a compound.
  • Difference from Molecular Formula: Often simpler; for ionic compounds, empirical and molecular formulae are identical.
  • Example:
    • Ethanoic Acid:
      • Molecular Formula: C₂H₄O₂
      • Empirical Formula: CH₂O

c. Ionic Compounds

  • Formation: Metals lose electrons to form cations; non-metals gain electrons to form anions.
  • Formula Determination:
    • Direct Comparison: Balances charges directly.
    • Swap-and-Drop Method: Swap the charge numbers of ions and drop the signs.
  • Example:
    • Iron(II) Sulfate: FeSO₄
    • Copper(II) Chloride: CuCl₂

d. Hydrated Salts

  • Definition: Ionic salts containing water molecules of crystallization.
  • Formula Representation: CuSO₄·5H₂O (5 water molecules)
  • Determination: By heating to remove water and calculating the ratio of water to salt.

2. Relative Masses

a. Relative Atomic Mass (Ar)

  • Definition: Average mass of atoms of an element relative to carbon-12.
  • Usage: Found on the Periodic Table.
  • Example:
    • Carbon (C): Ar = 12
    • Oxygen (O): Ar = 16

b. Relative Molecular Mass (Mr)

  • Definition: Sum of relative atomic masses of all atoms in a molecule.
  • Calculation: Add the Ar of each element multiplied by the number of atoms in the molecule.
  • Example:
    • Water (H₂O): Mr = (2×1) + 16 = 18

3. The Mole Concept

a. The Mole & Avogadro’s Constant

  • Mole (mol): Unit measuring the amount of substance.
  • Avogadro’s Constant: 1 mole = 6.02 × 10²³ particles (atoms, molecules, ions).
  • Molar Mass: Mass of 1 mole of a substance (g/mol).

b. Molar Volume of Gas

  • Avogadro’s Law: Equal moles of gases occupy equal volumes at the same temperature and pressure.
  • Molar Volume at RTP (20°C, 1 atm): 24 dm³/mol.
  • Conversions:
    • Volume (dm³) = Moles × 24
    • Volume (cm³) = Moles × 24,000

c. Linking Moles, Mass & Mr

  • Formula:
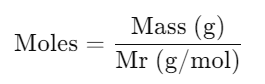
  • Usage: Calculate mass from moles or vice versa using the molar mass.

d. Limiting Reactants

  • Definition: Reactant that is completely consumed first, limiting the amount of product formed.
  • Determination Steps:
    1. Convert masses to moles.
    2. Use the balanced equation to find mole ratios.
    3. Identify the reactant that produces the least product.

4. Concentration of Solutions

a. Units of Concentration

  • Mass-Based: g/dm³
  • Mole-Based: mol/dm³

b. Calculating Concentration

  • Mass-Based Formula:
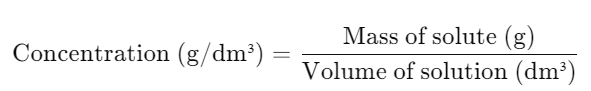
  • Mole-Based Formula:
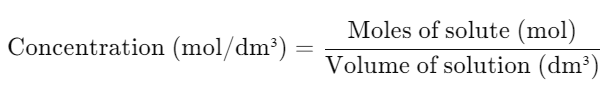
  • Conversions:
    • 1 dm³ = 1000 cm³
    • Convert units as necessary.

c. Titration Calculations

  • Purpose: Determine the concentration of an unknown solution by reacting it with a solution of known concentration.
  • Steps:
    1. Write and balance the reaction equation.
    2. Calculate moles of known solution.
    3. Use mole ratio to find moles of unknown.
    4. Calculate concentration of unknown.

5. Reacting Masses

a. Law of Conservation of Mass

  • Statement: Mass of reactants = Mass of products.
  • Application: Ensures balanced chemical equations.

b. Calculations Involving Masses

  • Steps:
    1. Balance the chemical equation.
    2. Convert masses to moles.
    3. Use mole ratios to find moles of desired substance.
    4. Convert moles back to mass using Mr.

c. Example Calculation

  • Reaction: 2Ca + O2​ → 2CaO
  • Given: 40 g Ca + 32 g O₂ → 80 g CaO
  • Verification: 80 g Ca + 32 g O₂ = 112 g CaO (Note: Ensure correct mole ratios in real calculations)

6. Percentage Calculations

a. Percentage Yield

  • Definition:
  • Importance: Measures efficiency of a reaction.
  • Example:
    • Actual Yield = 1.6 g
    • Theoretical Yield = 2.0 g
    • Percentage Yield:

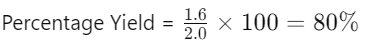
b. Percentage Composition

  • Definition: Mass of each element as a percentage of the total mass of the compound.
  • Formula:
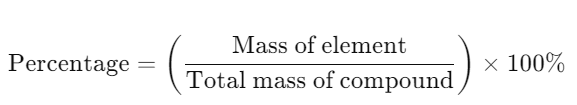
  • Example:
    • Water (H₂O):

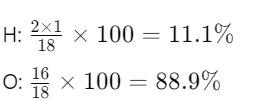
c. Percentage Purity

  • Definition:
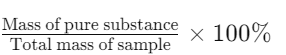
  • Example:
    • Pure Substance = 13.5 g
    • Total Sample = 15.0 g
    • Percentage Purity:

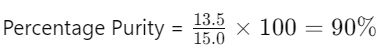
7. Empirical & Molecular Formulae

a. Calculating Empirical Formula

  • Steps:
    1. Convert mass of each element to moles.
    2. Divide all mole values by the smallest number of moles.
    3. If necessary, multiply to obtain whole numbers.
  • Example:
    • Given: 10 g H and 80 g O
    • Moles: H = 10/1 = 10; O = 80/16 = 5
    • Ratio: H₂O

b. Calculating Molecular Formula

  • Steps:
    1. Find the empirical formula.
    2. Calculate Mr of empirical formula.
    3. Divide Mr of molecular formula by Mr of empirical formula to find multiplier.
    4. Multiply subscripts in empirical formula by multiplier.
  • Example:
    • Empirical Formula: C₄H₁₀S
    • Mr Empirical: 90
    • Mr Molecular: 180
    • Multiplier: 180/90 = 2
    • Molecular Formula: C₈H₂₀S₂

8. Balancing Chemical Equations

a. Importance

  • Ensures the Law of Conservation of Mass is followed.
  • Equal number of each type of atom on both sides.

b. Methods

  • Trial and Error: Adjust coefficients to balance atoms.
  • Mole Ratio: Use the coefficients from the balanced equation for calculations.

c. Example

  • Unbalanced: Al + CuO → Al₂O₃ + Cu
  • Balanced: 2Al + 3CuO → Al₂O₃ + 3Cu

Exam Tips & Tricks

  • Always Balance Equations: Double-check atom counts on both sides.
  • Show All Workings: Even if the final answer is incorrect, partial credit may be awarded.
  • Use Formula Triangles: Helpful for memorizing relationships between concentration, moles, and volume.
  • Check Units: Ensure consistency, especially when converting between cm³ and dm³.
  • Understand Concepts: Memorization helps, but understanding application is crucial for problem-solving.

Worked Examples

1. Determining the Empirical Formula

  • Problem: 10 g H and 80 g O in a compound.
  • Solution:
    • Moles H = 10/1 = 10
    • Moles O = 80/16 = 5
    • Ratio H:O = 10:5 = 2:1
    • Empirical Formula: H₂O

2. Calculating Percentage Composition

  • Problem: Fe₂O₃ composition.
  • Solution:
    • Mass Fe = 2 × 56 = 112 g
    • Mass Fe₂O₃ = 2×56 + 3×16 = 160 g
    • % Fe = (112/160) × 100 = 70%

3. Balancing a Reaction

  • Problem: Al burns in Cl₂ to form AlCl₃.
  • Balanced Equation: 2Al + 3Cl₂ → 2AlCl₃

4. Titration Calculation

  • Problem: 25.0 cm³ HCl titrated with 12.1 cm³ 0.100 mol/dm³ NaOH.
  • Solution:
    • Moles NaOH = 0.0121 dm³ × 0.100 mol/dm³ = 0.00121 mol
    • Moles HCl = 0.00121 mol (1:1 ratio)
    • Concentration HCl = 0.00121 mol / 0.025 dm³ = 0.0484 mol/dm³
Table of Contents